
今回は、一階常微分方程式の中で最も基礎と言える、定数変化法を扱っていきます。
大学数学を初め、高校数学とのギャップに困っている方も、この記事を読むことで、「高校数学の延長」として理解することができます。
この記事を読み、「定数変化法」をマスターしていきましょう。
目次
一階線型微分方程式とは

まずは言葉の確認からしていきます。
一階線形微分方程式とは、次の形をとる、常微分方程式のことです。
$$y' + P(x)y=Q(x)・・・①$$
ここで一つ注意したいのが、「この形は変数分離形ではない」ということです。
変数分離形はこちら
上記ページで詳しく解説させていただきましたが、変数分離形は
$$\frac{dy}{dx} = g(x)・h(y)$$
すなわち
$$\frac{1}{h(y)}d(y) = g(x)d(x)$$
と変形し、この形から両辺積分をする形でした。
しかし①の一階線形微分方程式は、この形にできません。

そこで、以下のような解き方が必要となるのです。
一階常微分方程式の解き方
おおまかな流れは、こちらです。
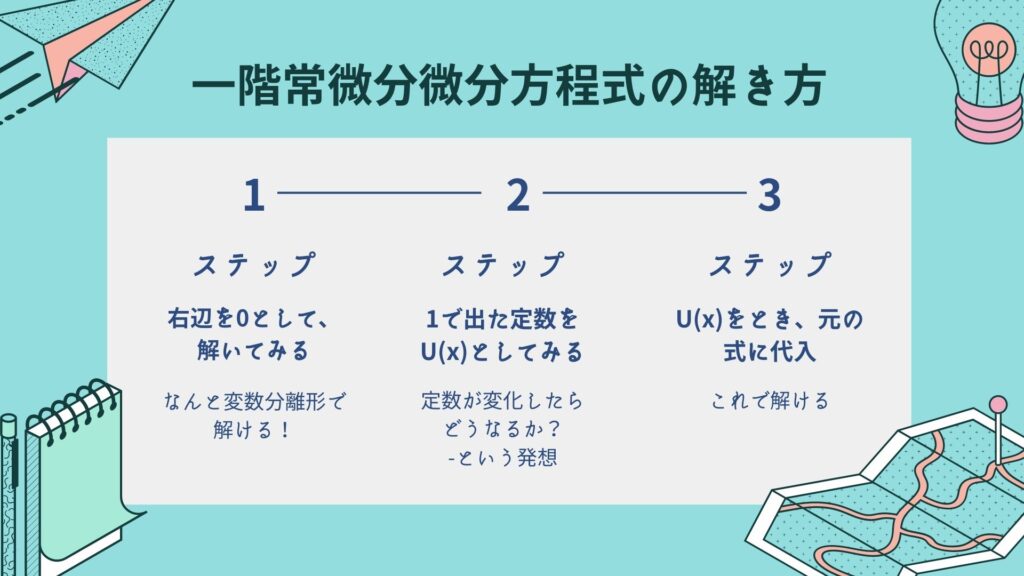
こうして求まる一般解は、
一階線形微分方程式 y'+P(x)y =Q(x) の一般解は
$$y = e^{ -\int_{}^{}P(x)dx } \left\{ \int_{}^{} Q(x) e^{ \int_{}^{}P(x)dx} +C \right\}$$
となります。
それでは、なぜこの一般解が求まるのかを順を追ってみていきましょう。
右辺を0とした、同伴方程式を解いてみる
まずは簡単のため、①でQ(x)=0としたものを解いてみましょう。
つまり、
$$ y' + P(x)y=0$$
を解いてみます。
ちなみにこの形は、同次方程式と言います。
$$y' + P(x)y=Q(x) (Q(x)=0) $$・・・②
を、同次方程式と言い、 さらに
「②は①の同伴方程式」ともいう。
それではこの同伴方程式
$$y' + P(x) y= 0・・・②$$
を解いてみます。
同伴方程式を見て気づくこと、それは
「①は変数分離形としては解けなかったが、②は変数分離形になっている!」
よって変数分離形の解き方を適用します。
\begin{eqnarray}
y' + P(x)y=&0 (ここで①よりy\neq 0)\\
y'=&-P(x)y\\
\frac{dy}{dx}=&-P(x)y\\
\int_{}^{}\frac {1}{y}dy =& -\int_{}^{}P(x)dx\\
log|y| =& -\int_{}^{}P(x)dx + C_1\\
|y| =& e^{-\int_{}^{}P(x)dx+ C_1}\\
y =& ± e^{C_1} ・e^{-\int_{}^{}P(x)dx }
\end{eqnarray}
ここで、簡単のために
$$ ±e^{C_1}=C_2(任意定数) $$と置きます。
すると②の一般解は
$$y = C_2・e^{ -\int_{}^{}P(x)dx }・・・③$$となりました!
これが、Q(x)=0と置いてみた時つまり同伴方程式の解となります。
非同次方程式を解いてみよう
②では、つまり一つ前の章では①でQ(x)=0として解きました。
その結果、
$$y = C_2・e^{ -\int_{}^{}P(x)dx }・・・③$$
を得ましたね。
ここでC2に注目してみましょう。
C2は任意定数、つまり任意に変わりうるということです。
ここで、C2がxによって任意に変わるとしたら?と考えることがミソです。
$$つまり、C_2がxについての関数、C_2=u(x)であったら、と考えてみます。$$
定数が変化していく...とする、この発想を「定数変化法」
といいます。
$$y = u(x)・e^{ -\int_{}^{}P(x)dx }・・・③'$$
これを元の式①に代入してみます。
③'を①に代入
$$\left\{ u(x)・e^{ -\int_{}^{}P(x)dx } \right\}' + P(x)・ u(x)・e^{ -\int_{}^{}P(x)dx } =Q(x)$$
$$ここで \left\{ u(x)・e^{ -\int_{}^{}P(x)dx } \right\}' =u'(x) ・e^{ -\int_{}^{}P(x)dx} +u(x) \left\{ e^{ -\int_{}^{}P(x)dx} \right\}' (積の微分) $$
$$= u'(x) ・e^{ -\int_{}^{}P(x)dx} + u(x)\left\{ -\int_{}^{}P(x)dx \right\}'・ e^{ -\int_{}^{}P(x)dx } (合成関数の微分)$$
$$= u'(x) ・e^{ -\int_{}^{}P(x)dx} - u(x) P(x)・e^{ -\int_{}^{}P(x)dx } $$
より、
$$ u'(x) ・e^{ -\int_{}^{}P(x)dx} - u(x) P(x)・e^{ -\int_{}^{}P(x)dx } + P(x)・ u(x)・e^{ -\int_{}^{}P(x)dx } =Q(x) $$
左辺の後ろ2つの項が打ち消しあって、結局
\begin{eqnarray}
u'(x) ・e^{ -\int_{}^{}P(x)dx} =& Q(x)\\
\frac {du}{dx}(x)=&Q(x) e^{ \int_{}^{}P(x)dx}
\end{eqnarray}
よって、両辺積分すれば
$$ u(x)= \int_{}^{} Q(x) e^{ \int_{}^{}P(x)dx} +C $$
u(x)が求まった!のでこれを③'に代入して
$$y = e^{ -\int_{}^{}P(x)dx } \left\{ \int_{}^{} Q(x) e^{ \int_{}^{}P(x)dx} +C \right\}$$
これが一般解です。
同伴方程式をとき、でた解の定数部を変化させ、代入することで一般解がもとまりました。
一階線形微分方程式の解き方【まとめ】
以上の流れとしては
1.同伴方程式(y'+P(x)y = 0)を解いてみると、変数分離形で解ける
2. 1において、定数が変化したらどうなる?という発想をする
3.定数をC=u(x)とおいてxの関数に置き換え、これを非同次方程式に代入してu(x)を求める
4.もとめたu(x)をもとの式に代入して、これを解けば一般解が求まる
となります。

以上、これを公式にすると
$$y' + P(x)y=Q(x)・・・①$$
の一般解は
$$y=e^{-\int_{}^{}P(x)dx}\left\{ {\int_{}^{}Q(x)e^{\int_{}^{}P(x)dx}dx+C}\right\}$$
お疲れ様でした!



















