
さて、この記事では三角関数の一番の基本の定理ともいえる加法定理を証明していきます。
1999年の東京大学入試問題でもありましたね。
加法定理を使って問題は解けるけど、その加法定理が成り立つ理由を説明できない、という受験生に対する警告だったのでしょうか…
目次
加法定理とは【復習】
加法定理には、以下の4つがありました。
sin(α+β)=sinαcosβ+cosαsinβ・・・(1)
sin(α-β)=sinαcosβ-cosαsinβ・・・(2)
cos(α+β)=cosαcosβ-sinαsinβ・・・(3)
cos(α-β)=cosαcosβ+sinαsinβ・・・(4)
こちら加法定理の4つですが、
(1),(2),(3)は(4)から、作ることができます。
そこで今回の記事は、この加法定理の(4)を図形・ベクトルを用いて導出することを解説して行きます。
ペンと紙を片手に、ぜひ手を動かしながら導出を真似してくださいね。
図形的に証明する【加法定理の証明:解法①】
<方針>cos(α-β)の形を作る。
そうすれば、図形的に何か見えてくるかもしれない。
<証明>
単位円上に二点 P,Qをとる。
OPとx軸、OQとx軸のなす角をそれぞれα,βとする。
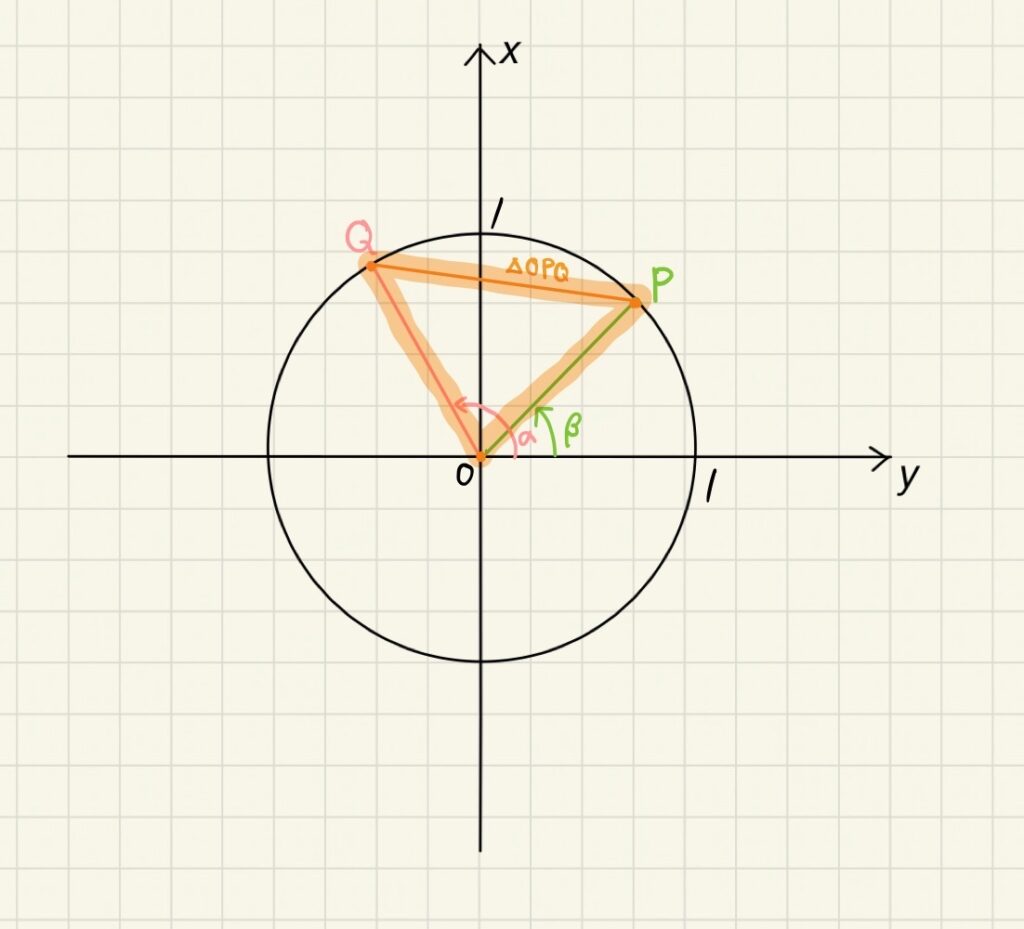
(PQは、余弦定理と座標の二通りで表せるな…!)
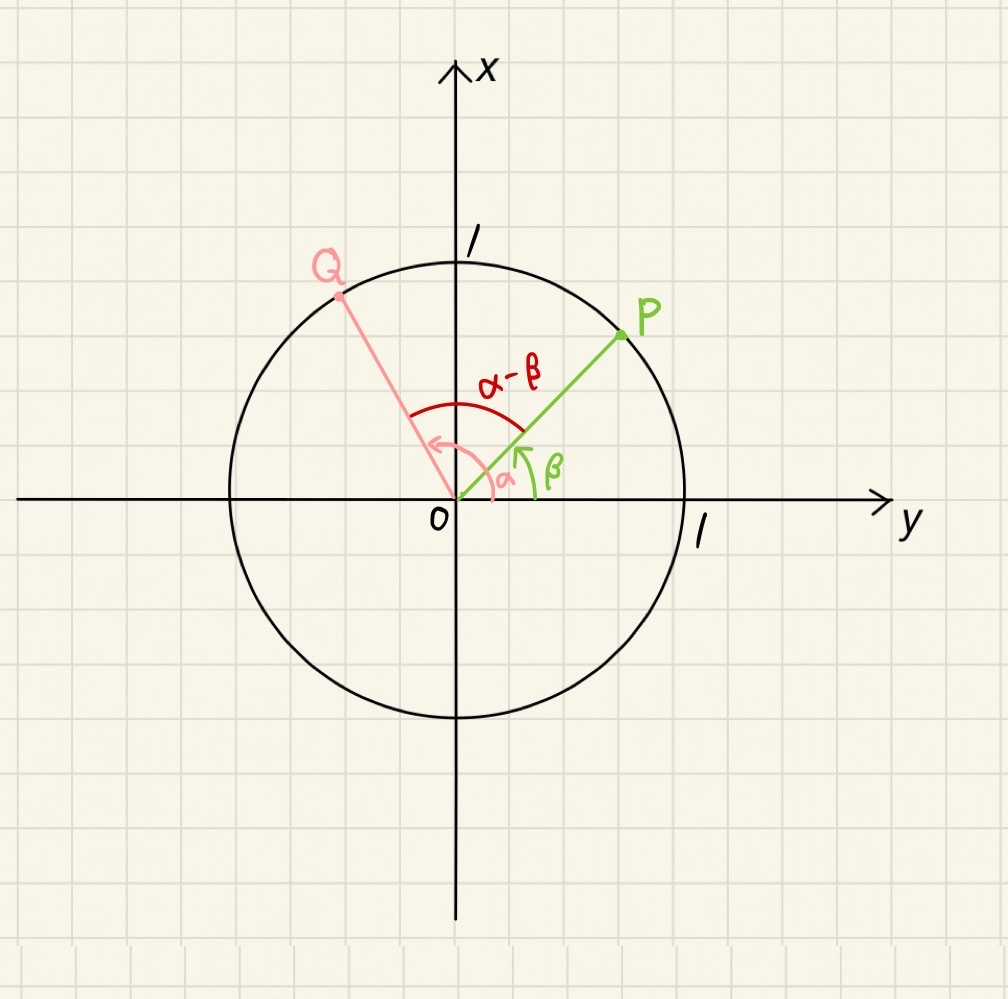
三角形OPQで余弦定理を用いると
\begin{eqnarray}
PQ^2&=&OP^2+OQ^2-2OP・OQcos(α-β) \\
&=&1+1-2cos(α-β)\\
&=& 2-2cos(α-β)---①
\end{eqnarray}
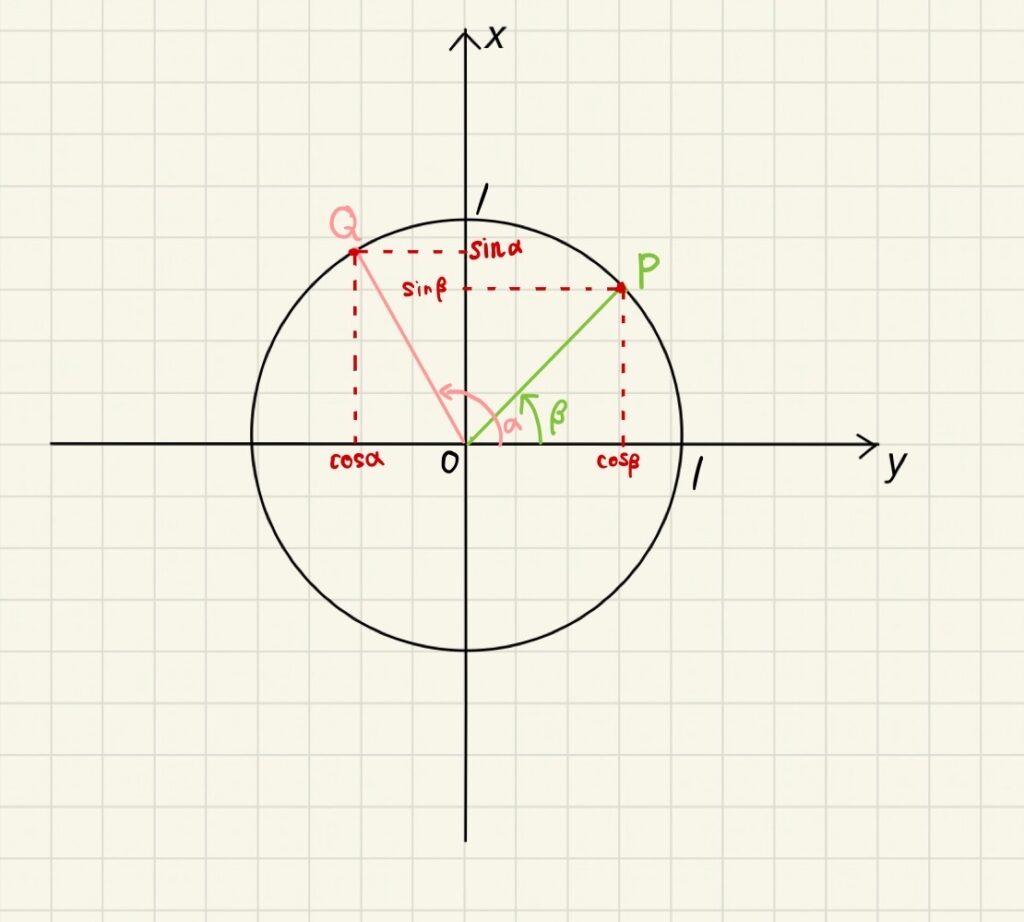
一方、線分PQの長さは、
\begin{eqnarray}
PQ^2&=&(cosβ-cosα)^2+(sinβ-sinα)^2 \\
&=&cos^2β-2cosβcosα+cos^2α+sin^2β-2sinβsinα+sin^2α\\
&=&(sin^2α+cos^2α)+(sin^2β+cos^2β)-2cosβcosα-2sinβsinα\\
&=&2-2(sinαsinβ+cosαcosβ)---②
\end{eqnarray}
①、②より、
$$2-2cos(α-β)=2-2(sinαsinβ+cosαcosβ)$$
これより
$$cos(α-β)=cosαcosβ+sinαsinβ$$
が成り立つ。
ベクトル(内積)を用いる【加法定理の証明:解法②】
図のようにP,Qをとる。
この時、P,Qの座標はそれぞれ(cosβ,sinβ)、(cosα,sinα)と表される。
内積の定義から、
P・Q=|P||Q|cos(α-β)
=1・1・cos(α-β)
=cos(α-β)・・・①
一方、成分表示で内積を求めると、
$$P・Q=P_{x}・Q_{x}+P_{y}・Q_{y}$$
=cosαcosβ+sinαsinβ・・・②
①、②より
cos(α-β)=cosαcosβ+sinαsinβ
が成り立つ。
まとめ
いかがだったでしょうか。
今回は図形的なやり方、ベクトルの内積を用いたやり方の2通りで加法定理の導出を行いました。
加法定理の定義、導出をしておくことは見落としがちですが、大切です。
是非今回でマスターしておきましょう。

















