
オイラーの公式って有名だよね!ちょっと勉強してみたいな。
オイラーの公式を勉強したいけど、難しそう…
今回の記事では、そんな気持ちの大学生・高校生に向けて、簡単かつ分かりやすく「オイラーの公式」を解説していきます。
高校数学の三角関数を知っているなら理解できる内容を紹介するので、ぜひ構えず見ていってくださいね。
この記事を読むことで、オイラーの公式が成り立つことを説明できるようになります!
目次
オイラーの公式とは
オイラーの公式とは、
$$e^{ix} = \cos x + i \sin x $$
で表される公式です。
ロジャー・コーツの見出した、
$$log (\cos x + i \sin x) = ix$$
という対数関数の形の公式が元になったと言われています。
この公式を、指数関数の形にした人がオイラーなのですね。
$$log (\cos x + i \sin x) = ix$$
を指数関数の形にすると
$$e^{ix} = \cos x + i \sin x $$
となります。
この公式は、複素数と実数の項をそれぞれもっていますから、複素数と実数を結びつけることができます。
そんなオイラーの公式は、かの天才、リチャード・ファイマンに「我々の至宝かつ最も素晴らしい公式」と言わしめました。
オイラーの公式はどんなところで使われているか
オイラーの公式は、数学にとどまらず、工学や物理学など本当に多くの分野で使われています。
ここではそのうちの少しだけ紹介しますので、オイラーの公式の凄さを体感してもらえればと思います。
オイラーの公式をじっくりと見てください。
$$e^{ix} = \cos x + i \sin x $$
左辺は指数関数、右辺は三角関数を使って表されています。
どうやら、
三角関数を指数関数にするまたは指数関数を三角関数にする
ということができそうですね。
これが、オイラーの公式が威力を発揮しやすいところを一つ、示してくれています。
三角関数とは、波を表すものでしたね。
ということは、波を、三角関数ではなく指数関数を使って表せる様になるということです。
「波を三角関数ではなく指数関数を使って表せること」の利点は、一つは計算がしやすくなるということです。
三角関数は微分積分によって、sinとcosがいれかわり形が変わってしまい、煩雑です。
(その他位相と振幅などの利点もありますが、物理学の知識が必要になるため、この記事では省略させて頂きます。)
三角関数を指数関数へ変換するオイラーの公式は、波の位相を振幅で扱うことができ、計算がしやすくなるため、「波が登場する分野ではほぼ使われている」といえるのではないでしょうか。
ちなみにこの記事の最後では、オイラーの公式を用いて、三角関数の加法定理を導いています。
興味のある方はぜひ御覧ください。
オイラーの公式が成り立つ事を証明してみよう
ついに、この記事の山場にやってきました。
オイラーの公式が成り立つことを説明できるようになりましょう。
<目標>
オイラーの公式$$e^{ix} = \cos x + i \sin x $$が成り立つことを説明できる様になる
<方針>
マクローリン展開を使うことで、左辺を式変形。右辺も式変形して、同じ形を作り出すこと
(A=C,B=CよってA=Bとする)
左辺をマクローリン展開すると、
\begin{eqnarray}
e^{ix} &=& \sum_{k=0}^∞ \frac{{ix}^k}{k!} \\
&=&1 + \frac{ix}{1!} + \frac{{ix}^2}{2!} + \frac{{ix}^3}{3!} + \frac{{ix}^4}{4!} + ・・・\\
&=& 1 + ix - \frac{{x}^2}{2!} - \frac{{ix^3}}{3!} + \frac{{x}^4}{4!}+ ・・・
\end{eqnarray}
見やすくするために、実部と虚部で分けます。
$$= (1 - \frac{{x}^2}{2!} + \frac{{x}^4}{4!} + ・・・)+ i(x - \frac{{x^3}}{3!} ・・・) ① $$
つぎは右辺です。
sin x と cos x のマクローリン展開をします。
\begin{eqnarray}
cos x + i \sin x &=& \sum_{k=0}^∞ (-1)^k \frac{{x}^{2k+1}}{{2k+1}!} + i \sum_{k=0}^∞ (-1)^k \frac{{x}^{2k}}{{2k}!}\\
&=& (1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ・・・) +i (\frac{x}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} ・・・) ②
\end{eqnarray}
①と②が一致しましたね!
これで、オイラーの公式$$e^{ix} = \cos x + i \sin x $$が成り立つことを、式変形により説明できるようになりましたね!
更に、オイラーの等式を知ろう
オイラーの公式から、円周率π、複素数、実数、ネイピア数eをつなぎ合わせる等式が導かれます。
この一見関係なさそうな「π、i、実数、e」に実は深い関係があって、互いに関係しあっている…
ということの不思議さをぜひ知って頂きたいと思います。
それでは行きましょう。
まずは$$e^{ix} = \cos x + i \sin x $$のxにπを代入します。
$$e^{i π} = \cos π + i \sin π$$
ここで sin π は 0 、 cos π は -1 ですから
\begin{eqnarray}
e^{i π} &=& -1\\
e^{i π} + 1 &=& 0
\end{eqnarray}
どうでしょう!見事にe、i、π がつながりました。
シンプルな見た目ですね。
オイラーの公式を用いて、三角関数の加法定理を導こう
三角関数の基本ともいえる加法定理ですが、なんとオイラーの公式から簡単に導くことができます。
もちろん高校生レベルで、ということであれば、図形的な話に持ち込んだり、、、とかいろいろやり方はあるんですが、面倒です。
そちらも解説しているので、気になる方はこちらをどうぞ。
sin(α+β)=sinαcosβ+cosαsinβ・・・(2)
cos(α+β)=cosαcosβ-sinαsinβ・・・(4)
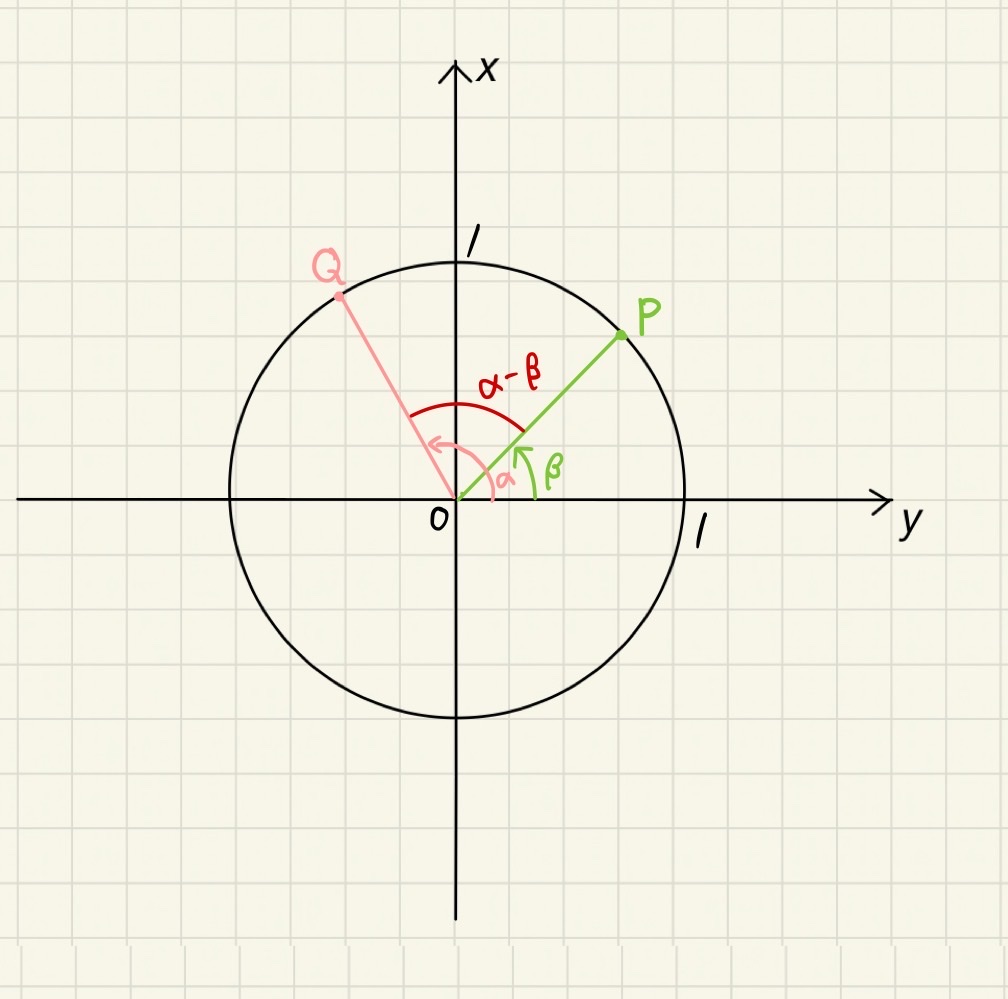
を導いていこうと思います。
まずは、オイラーの公式で、x = α + β を代入します。
$$e^{i{\alpha + \beta}} = \cos (\alpha + \beta) +i \sin (\alpha + \beta)$$
ここで、指数法則を用いると、左辺は
$$e^{i{\alpha + \beta}} = e^{i \alpha}e^{i \beta}$$
ここにもオイラーの公式を使って
\begin{eqnarray}
e^{i \alpha}e^{i \beta}
&=&(\cos \alpha + i \sin \alpha)(\cos \beta+ i \sin \beta)\\
&=& (\cos \alpha \cos \beta -\sin \alpha \sin \beta) + i (\sin \alpha \cos \beta + \cos \alpha \sin \beta)\\
\end{eqnarray}
どうでしょう。これを右辺と、実部虚部それぞれ比べてください。
虚部$$\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$
実部$$\cos (\alpha + \beta) = \cos \alpha \cos \beta -\sin \alpha \sin \beta$$
加法定理が導かれました!!
この手法ができれば、、、と1999年東京大学数学第一問で涙をのんだ人もいるでしょう、、
それはともかく、オイラーの公式を使って、ここまで簡単に加法定理を導くことができましたね。
まとめ
この記事では、オイラーの公式とはなにかということから、公式の証明、さらにはオイラーの等式についても触れました。
高校数学までは、三角関数、指数関数、πなどは別分野として教わってきました。
それらの項目が繋がり合うのが、集大成のようで達成感がありますよね。
ぜひ覚えておいてくださいね。


















