
今回のブログでは、Gray-Scottモデルと呼ばれるモデルを知り、興味を持って調べたことを解説していきます。
人工生命:Artificial Lifeと呼ばれる領域に興味を持ち、「ALife 実装を通した人工生命モデル理論入門」というオライリー出版の本を勉強した中で出てきた事項です。
Gray-Scottモデルは、P.GrayとS.K.Scottによって考案されました。
自然界に存在するさまざまな模様が、このモデルを使ったシュミレーションで再現することができます。
「シンプルなモデルで、さまざまな模様を生成することができる」という点が非常に面白いのでぜひ読んでいただけると幸いです。
目次
学習の動機
- 自然現象の理解:
- Gray-Scottモデルは、生物学的な模様や化学的なパターンなど、自然界の複雑な現象を理解するための強力なツールである。
- 数学と科学の融合:
- このモデルは数学的な美しさと科学的な実用性を兼ね備えており、両分野の知識を深める絶好の機会となる。
- コンピュータシミュレーションへの応用:
- コンピュータグラフィックスを用いた応用は、技術的なスキルを磨く上で非常に有益である。
この記事を読むことで、以下の事項に触れることができます。
学習のロードマップ
- 基礎概念の理解:
- 数学的な基礎:偏微分方程式、ラプラシアン、拡散過程など。
- 科学的な基礎:化学反応、生物学的パターン形成、拡散プロセスなど。
- 方程式の研究:
- Gray-Scottモデルの偏微分方程式を理解し、各項の意味と影響を学ぶ。
- シミュレーションツールの習得:
- Processing、Pythonなどのプログラミングを通して、2Dシミュレーションを行う
はじめに:Gray-Scottモデルとは

科学と数学に触れながら学ぶことができるGray-Scottモデルについて探求する旅にようこそ。
このモデルは、化学反応と拡散のプロセスを通じて、自然界のさまざまなパターン形成を説明するために用いられます。
今回のブログでは、このモデルの基本原理から応用例、さらには実装まで、モデルを紐解いていきます。
Gray-Scottモデルの基本概念
Gray-Scottモデルは、化学物質の反応と拡散をモデル化したもの1つです。
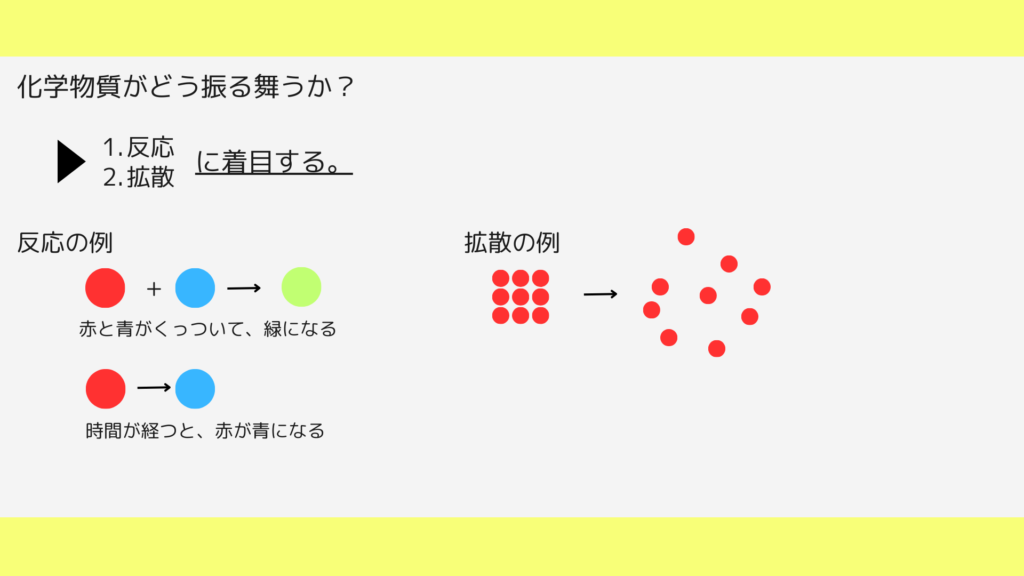
Gray-Scottモデルでは、2つの物質について考えます。
このモデルでは、二つの化学物質が相互作用し、時間が経過すると共に様々なパターンを生成することがわかっています。
そしてこのモデルを用いたシュミレーションで、生物学的な模様に現れることがわかっているのです!
例えば、以下のちょうちょの羽、シマウマの縞などの模様が、拡散・反応した分子の分布として生成されます。


Pixabyより
より詳しくみていこう
Gray-Scottモデルは、反応拡散系の一つで、特定の化学反応と物質の拡散を模倣した数学モデルです。
具体的には、Gray-Scottモデルでは次の二つの物質を考えます。:
- U物質:この物質は自己複製能力を持ち、特定の条件でV物質に変換されます。
- つまり、量が少なくなってきたら、自分を複製し増やしますor追加され、一定量になるように頑張る
- V物質によって、U物質がV物質になる
- V物質:この物質はU物質の成長を抑制し、U物質が一定の閾値を超えるとこれを分解します。
- V物質によって、U物質がV物質になります。
- 増えすぎると、一定量まで減るように調整されます
U物質とV物質は時間が経つとだんだん広がっていき(拡散)、広がった先でU物質とV物質が出会うと反応を起こすというわけです。
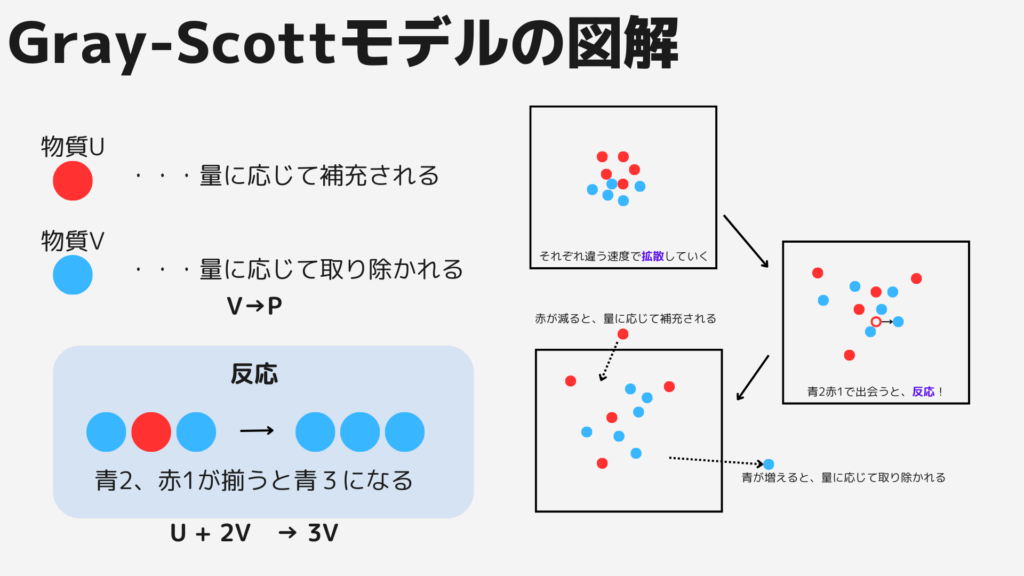
U物質、V物質の拡散速度や反応速度によって、それぞれの物質の広がり方が変わってきますよね。
また、物質の量も変わってきそうです。
そのため、物質の広がり方や量によって、その形作る模様がかわるのです!
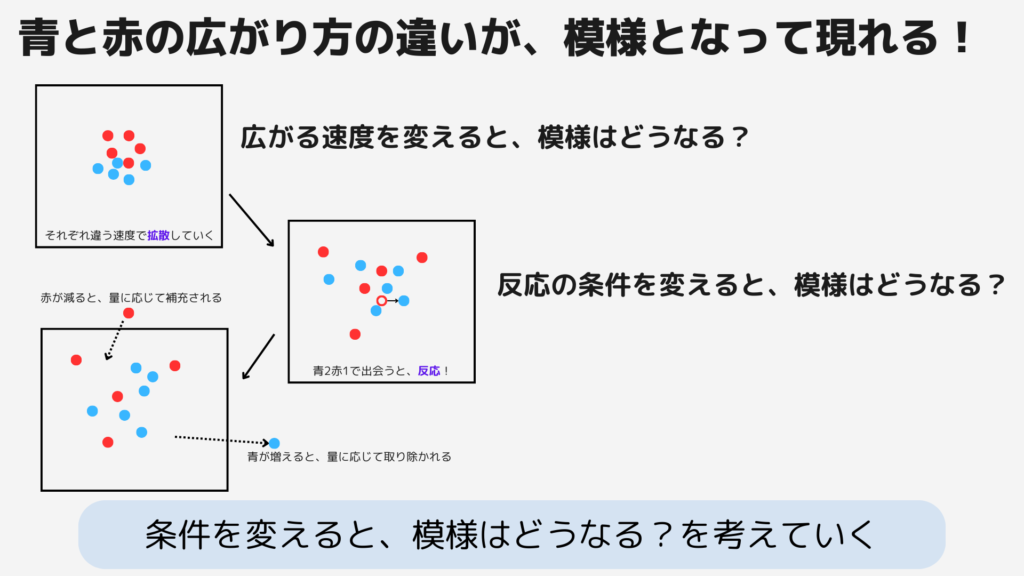
実際には、条件を変えていくと、このようなシュミレーションとして、物質の模様が見えます。
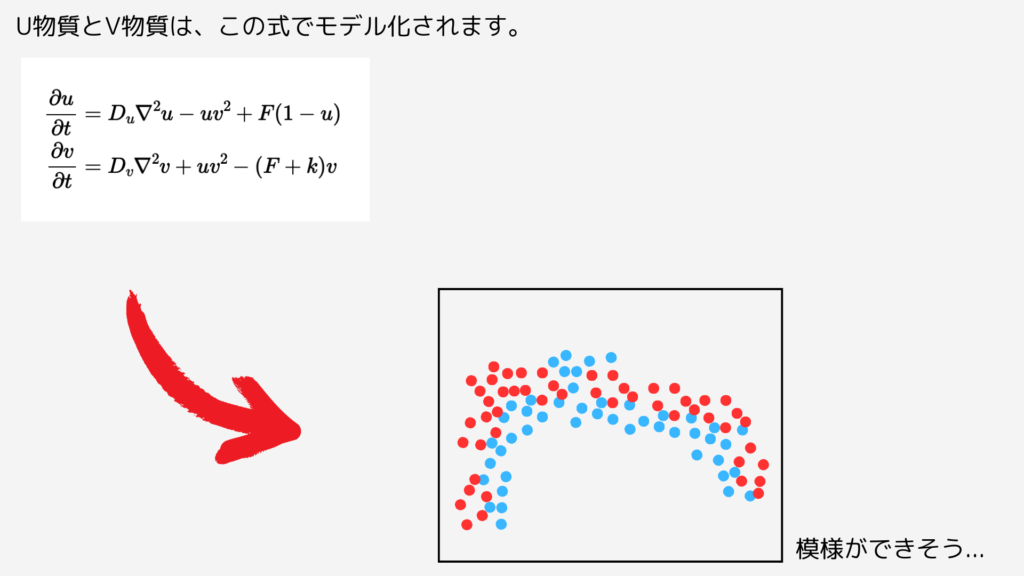
なかなか不思議ですよね。
Gray-Scottモデルの興味深い点は、特定のパラメータの値において、非常に複雑で美しいパターンや構造を生み出すことがあります。
そして書籍では、これらのパターンは生物学的な模様形成や、特定の化学反応における現象を理解する上で重要な示唆を与えると指摘されていました。
モデルの数学的背景
このモデルの方程式は以下のようになります:
\begin{align} \frac{\partial u}{\partial t} &= D_u \nabla^2 u - uv^2 + f(1 - u) \\ \frac{\partial v}{\partial t} &= D_v \nabla^2 v + uv^2 - (f + k)v \end{align}
ここで、$u$と$v$はそれぞれU物質とV物質の濃度、$D_u$と$D_v$はそれぞれの拡散係数、$f$と$k$は反応を制御するパラメータです。
fは補充(feed)、kは減少(kill)からきていると考えるとわかりやすいですね。
このモデルは、通常、二つの化学物質(UとVとする)の濃度に関する偏微分方程式で表されます。
微分方程式って何?という方は、丁寧に解説していますのでぜひこちらをご覧ください。
核となるのは、二つの偏微分方程式です。
- 拡散項: $D_u \nabla^2 u$と$D_v \nabla^2 v$
- これらはU物質とV物質の拡散を表す項です。
- $D_u$, D_v$は拡散係数と呼ばれ、拡散の程度を表す、物質ごとに定める定数です。
- 簡単のため、相互作用がないとした時の影響はどうなるかを考えておきましょう。
- 増加の影響: 拡散係数を増やすと、物質はより速く拡散するようになります。つまり、模様はより広範囲に拡がります。
- 減少の影響: 拡散係数を減らすと、物質の拡散は遅くなります。より局所的な模様が形成されそうです。
- $\nabla^2$は、ラプラシアン演算子と呼ばれます。難しそうな内容ですが、ここでは「ある点でとその周りが、どれくらい変化しているか」を表すものだと思ってください。
- 反応項: $- uv^2 $と$+ uv^2 $
- これらはU物質とV物質の相互作用を示す項です(uv^2になる理由は、反応速度式からきています)。
- Uについて記述している上の式では、物質U はuv^2で減っています。
- Vについて記述している下の式では、物質U はuv^2で増えています。
- V物質のFeed項: $- (f + k)v $
- V物質が増えすぎた時の、V物質の減少を示します。vの量と、補充量の定数f+減少量の定数kの積になっています。
- 増加の影響: kまたはfを増やすと、V物質の減少が加速し、U物質の優位が強まります。沢山物質uを追加したり、物質vを大きく減らすと、Uが多くなるということですね。
- 減少の影響: kまたはfを減らすと、V物質の減少が緩やかになり、より安定した状態が保たれます。
- U物質の自然減少項: $f(1 - u) $
- u物質が減りすぎた時の、u物質の増加(自己複製)を示します。補充量の係数fと、uの残量の積uの関係で表されます。(1-u)というのは、uが少ないほど補充が活発になり、uが多いほど補充量は少ないということですね。
ラプラシアン演算子について
ラプラシアンは、あるスカラー関数 $f $に対して、その関数の全ての空間的方向における二階の偏微分の和として定義されます。
3次元空間において、ラプラシアン$\nabla^2 f $は次のように表されます:
$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}$
つまり、ある点fと、その周囲の傾きの変化量を表しているのですね。
特定の点周辺のスカラー関数とは、空間内の各点において単一の数値(スカラー値)を持つ関数です。
これは、空間の各点における温度、圧力、濃度など、一つの数値によって表される物理量の分布を示します。
特定の点周辺のスカラー関数は、空間内での物理量の分布を表すための基本的なツールです。
ラプラシアンを含む微分演算子を適用することで、これらの分布のより詳細な特性や挙動を理解することができます。
ラプラシアンが大きいというのは、「関数の値がその点の周囲で急激に変化している:例えば温度分布においてラプラシアンの大きい点というとき、その周辺で急激な温度勾配があることを示している」というイメージです。
Gray-Scottモデルでは、これらのパラメータを調整することで、様々な複雑なパターンを生成することができます。
これらのパターンは、パラメータの微妙な変化によっても大きく異なることがあります!
「パラメータを少し変えると、模様が全然異なって見える!」ということがあり、モデルのダイナミックな性質を示していて面白いと感じました。
生物学的パターン形成への応用
Gray-Scottモデルは、動物の皮膚の模様や貝殻の独特なデザインなど、自然界の多様なパターンの生成メカニズムを理解するのに用いられるそうです。
これらのパターンは、体内の化学物質間の複雑な相互作用によって形成されているのですね。
キリンや貝殻、熱帯魚を表皮を見て、「小さな色素細胞、色素物質を取り巻く生体内の相互作用によってそれらキリンや貝殻、熱帯魚の皮膚模様が作られているのではないか」と想像すると、非常に好奇心を掻き立てられますよね...!
実装
ProcessingやPythonを用いて、Gray-Scottモデルを実装することができます。
今回はProcessingを使用した際の、コード例を表示させていただきますね。
Processingを使用した基本的な実装例
int size = 50; // グリッドのサイズ
float[][][] A = new float[size][size][size];
float[][][] B = new float[size][size][size];
float dA = 1.0;
float dB = 0.5;
float feed = 0.055;
float k = 0.062;
void setup() {
size(200, 200, P3D);
// 初期化
for (int x = 0; x < size; x++) {
for (int y = 0; y < size; y++) {
for (int z = 0; z < size; z++) {
A[x][y][z] = 1;
B[x][y][z] = 0;
}
}
}
// B物質の初期配置
for (int x = size / 2 - 5; x < size / 2 + 5; x++) {
for (int y = size / 2 - 5; y < size / 2 + 5; y++) {
for (int z = size / 2 - 5; z < size / 2 + 5; z++) {
B[x][y][z] = 1;
}
}
}
}
void draw() {
background(51);
// 3D表示
translate(width/2, height/2);
rotateY(0.01 * frameCount);
scale(4);
for (int x = 1; x < size - 1; x++) {
for (int y = 1; y < size - 1; y++) {
for (int z = 1; z < size - 1; z++) {
float a = A[x][y][z];
float b = B[x][y][z];
float diffA = dA * laplace(A, x, y, z);
float diffB = dB * laplace(B, x, y, z);
float reaction = a * b * b;
float feedRate = feed * (1 - a);
A[x][y][z] = a + (diffA - reaction + feedRate);
B[x][y][z] = b + (diffB + reaction - (k + feed) * b);
// カラーと位置の設定
if (A[x][y][z] - B[x][y][z] > 0.25) {
pushMatrix();
translate(x - size / 2, y - size / 2, z - size / 2);
fill(255, 255 * b, 255 * a);
box(1);
popMatrix();
}
}
}
}
}
float laplace(float[][][] grid, int x, int y, int z) {
float sum = 0;
sum += grid[x][y][z] * -1;
sum += grid[x-1][y][z] * 0.2;
sum += grid[x+1][y][z] * 0.2;
sum += grid[x][y-1][z] * 0.2;
sum += grid[x][y+1][z] * 0.2;
sum += grid[x][y][z-1] * 0.2;
sum += grid[x][y][z+1] * 0.2;
sum += grid[x-1][y-1][z] * 0.05;
sum += grid[x+1][y-1][z] * 0.05;
sum += grid[x+1][y+1][z] * 0.05;
sum += grid[x-1][y+1][z] * 0.05;
sum += grid[x-1][y][z-1] * 0.05;
sum += grid[x+1][y][z-1] * 0.05;
sum += grid[x+1][y][z+1] * 0.05;
sum += grid[x-1][y][z+1] * 0.05;
sum += grid[x][y-1][z-1] * 0.05;
sum += grid[x][y+1][z-1] * 0.05;
sum += grid[x][y+1][z+1] * 0.05;
sum += grid[x][y-1][z+1] * 0.05;
return sum;
}
まとめと今後の展望
今後の研究や応用への可能性
このモデルの可能性は計り知れず、今後の研究や技術開発においてさらなる応用が期待されます。自然界の美しさと複雑さを数学的に理解する旅は、まだまだ続きます。
このブログが、Gray-Scottモデルの魅力と重要性を理解する一助となれば幸いです。




















